Reliability (statistics)
In statistics, reliability is the consistency of a set of measurements or of a measuring instrument, often used to describe a test. Reliability is inversely related to random error.[1]
Contents |
Types
There are several general classes of reliability estimates:
- Inter-rater reliability is the variation in measurements when taken by different persons but with the same method or instruments.
- Test-retest reliability is the variation in measurements taken by a single person or instrument on the same item and under the same conditions. This includes intra-rater reliability.
- Inter-method reliability is the variation in measurements of the same target when taken by a different methods or instruments, but with the same person, or when inter-rater reliability can be ruled out. When dealing with forms, it may be termed parallel-forms reliability.[2]
- Internal consistency reliability, assesses the consistency of results across items within a test.[2]
Difference from validity
Reliability does not imply validity. That is, a reliable measure is measuring something consistently, but you may not be measuring what you want to be measuring. For example, while there are many reliable tests of specific abilities, not all of them would be valid for predicting, say, job performance. In terms of accuracy and precision, reliability is analogous to precision, while validity is analogous to accuracy.
An example often used to illustrate the difference between reliability and validity in the experimental sciences involves a common bathroom scale. If someone who is 200 pounds steps on a scale 10 times and gets readings of 15, 250, 95, 140, etc., the scale is not reliable. If the scale consistently reads "150", then it is reliable, but not valid. If it reads "200" each time, then the measurement is both reliable and valid. This is what is meant by the statement, "Reliability is necessary but not sufficient for validity."
Estimation
Reliability may be estimated through a variety of methods that fall into two types: single-administration and multiple-administration. Multiple-administration methods require that two assessments are administered. In the test-retest method, reliability is estimated as the Pearson product-moment correlation coefficient between two administrations of the same measure: see also item-total correlation. In the alternate forms method, reliability is estimated by the Pearson product-moment correlation coefficient of two different forms of a measure, usually administered together. Single-administration methods include split-half and internal consistency. The split-half method treats the two halves of a measure as alternate forms. This "halves reliability" estimate is then stepped up to the full test length using the Spearman–Brown prediction formula. The most common internal consistency measure is Cronbach's alpha, which is usually interpreted as the mean of all possible split-half coefficients.[3] Cronbach's alpha is a generalization of an earlier form of estimating internal consistency, Kuder-Richardson Formula 20.[3]
These measures of reliability differ in their sensitivity to different sources of error and so need not be equal. Also, reliability is a property of the scores of a measure rather than the measure itself and are thus said to be sample dependent. Reliability estimates from one sample might differ from those of a second sample (beyond what might be expected due to sampling variations) if the second sample is drawn from a different population because the true variability is different in this second population. (This is true of measures of all types—yardsticks might measure houses well yet have poor reliability when used to measure the lengths of insects.)
Reliability may be improved by clarity of expression (for written assessments), lengthening the measure,[3] and other informal means. However, formal psychometric analysis, called item analysis, is considered the most effective way to increase reliability. This analysis consists of computation of item difficulties and item discrimination indices, the latter index involving computation of correlations between the items and sum of the item scores of the entire test. If items that are too difficult, too easy, and/or have near-zero or negative discrimination are replaced with better items, the reliability of the measure will increase.
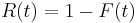 .
.
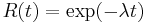 . (where
. (where  is the failure rate)
is the failure rate)
Classical test theory
In classical test theory, reliability is defined mathematically as the ratio of the variation of the true score and the variation of the observed score. Or, equivalently, one minus the ratio of the variation of the error score and the variation of the observed score:
where 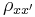 is the symbol for the reliability of the observed score, X;
is the symbol for the reliability of the observed score, X; 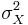 ,
, 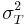 , and
, and 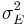 are the variances on the measured, true and error scores respectively. Unfortunately, there is no way to directly observe or calculate the true score, so a variety of methods are used to estimate the reliability of a test.
are the variances on the measured, true and error scores respectively. Unfortunately, there is no way to directly observe or calculate the true score, so a variety of methods are used to estimate the reliability of a test.
Some examples of the methods to estimate reliability include test-retest reliability, internal consistency reliability, and parallel-test reliability. Each method comes at the problem of figuring out the source of error in the test somewhat differently.
Item response theory
It was well-known to classical test theorists that measurement precision is not uniform across the scale of measurement. Tests tend to distinguish better for test-takers with moderate trait levels and worse among high- and low-scoring test-takers. Item response theory extends the concept of reliability from a single index to a function called the information function. The IRT information function is the inverse of the conditional observed score standard error at any given test score.
See also
- Coefficient of variation
- Homogeneity (statistics)
- Internal consistency
- Levels of measurement
- Accuracy and precision
- Reliability disambiguation page
- Reliability theory
- Reliability engineering
- Reproducibility
- Validity (statistics)
References
Rousson, V., Gasser, T., and Seifer, B. (2002). "Assessing intrarater, interrater and test–retest reliability of continuous measurements" Statistics in Medicine, 21(22): 3431–3446. http://dx.doi.org/10.1002/sim.1253